Iteration

Programs usually work through a sequence of programming language statements in some repetitive manner until some condition is satisfied and the repetition stops.  The repetition can be written in code in several ways:  as a loop or as a recursion.

There is a theorem in mathematics of computing that states that the program code for any loop can be transformed into a recursive code and vice-versa.  Loops are almost “intuitive” to understand, but what is recursion?

Example

A simple example of an iterative computation:  calculate the function n! (n-factorial)

n! is defined as the product of all integers from n down to 1.

Thus 3!=3×2×1=6, 12!=12×11×10×9×8×7×6×5×4×3×2×1 = 479'001'600

We multiply the successive numbers until we reach 1, where we stop. Reaching 1 is the condition that halts the iteration.

Code expressing that computation in code could be:

Line 2 starts of the container V with the innocuous value 1.  Then in lines 3 to 5 there is a repeat-loop, using a container i which starts out at value N, and then each time around the loop will be decremented by 1 until comes down to 1.  The statement in line 4 will multiply V by the value of i, and hence at the end V will contain N!.

The result is then returned.

Recursion

But we can do this in a more elegant way, by observing that N! = N×(N-1)!.  I.e. the factorial for any number is that number times the factorial for the just preceding number.

For example, if we know 12!=12×11×10×9×8×7×6×5×4×3×2×1 then we know that 13!=13×12×11×10×9×8×7×6×5×4×3×2×1 = 13×12!

Putting this into code:

Let's see what happens if we use this recursive function to compute 3!:

We ask for Factorial(3).  The if-statement on line 2 tests to see if 3=1, which of course is false, and therefore it computes 3×Factorial(2) instead.
That is an imcomplete computation, since we have to call the function again, now with a smaller number.  We ask for the value of Factorial(2), coming in at line 1 again, but now with N=2.  The if-statement tests again, 2 is not equal 1, so it computes now 2xFactorial(1).
That comes in at line 1 again, but now the if-statement finds that 1=1, and therefore it returns 1 to the still incomplete computation of 2×Factorial(1) which now becomes 2×1 or 2.
That value of 2 is returned to the also still incomplete computation of 3×Factorial(2) which becomes 3×2 or 6.  And that completes the computation of Factorial(3):  it is 6.

Inside the machine code the implementation of the function will use a “stack” to hold information about the as yet incomplete computations.  This stack is literally a pile of incomplete intermediate computations, which will be “popped off” the stack as results become available.

Interesting difference

If we calculate N! for a large number, say 10'000, then there must be enough memory allocated to hold the value of 10'000!  That is of course so for both the iterative and the recursive solution.  But in the recursive solution there must also be enough memory to hold a stack of 9'999 incomplete intermediate computations, which may be much more than available.

Therefore recursion may take less code, but it may take a lot more memory and also a longer execution time, needed for managing the recursion stack.

A non-trivail Example

This whole page was prompted by a problem posed as the “weekly puzzle” at CERN's IdeaSquare in April 2025.

The puzzle was about travelling on a railway system:

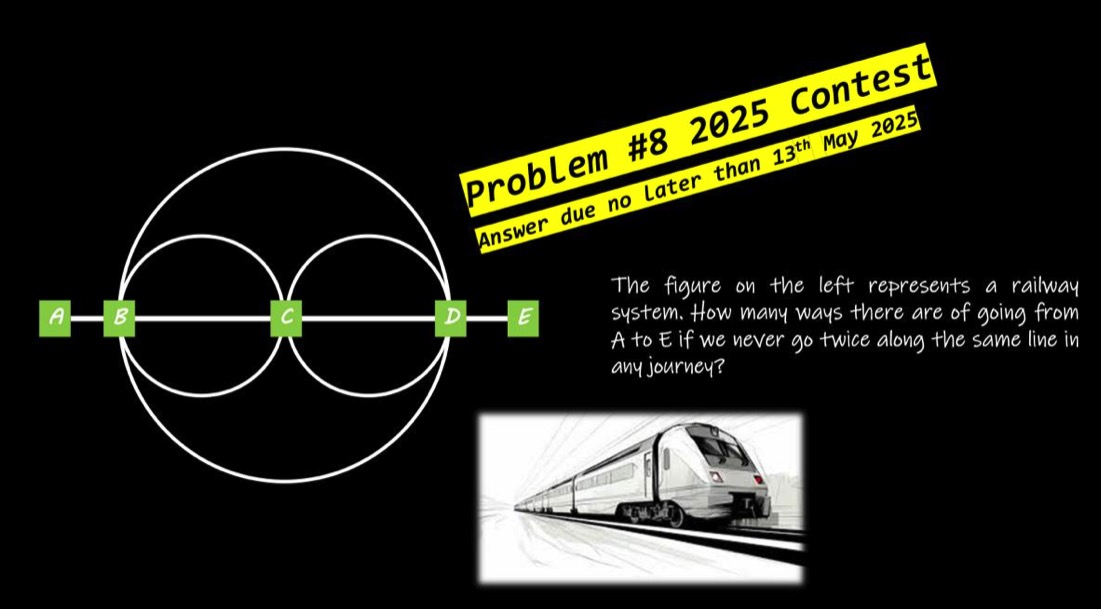
In the following diagram I labelled the stations differently and also gave names to the tracks:

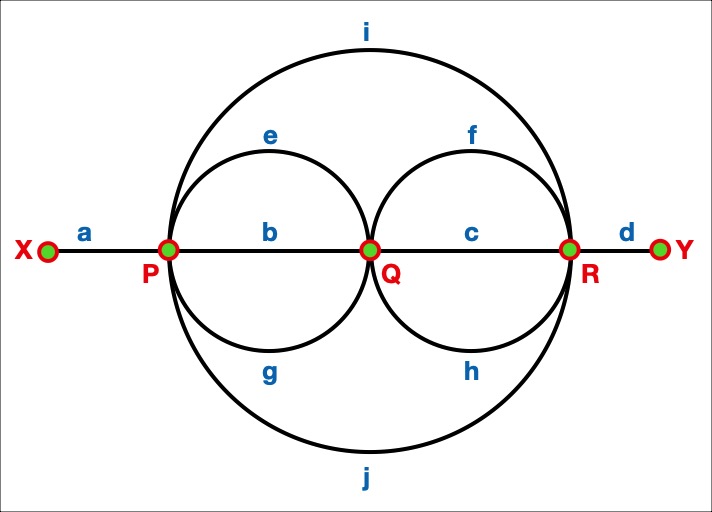
There are five stations called X, P, Q, R and Y.  They are connected by railroad tracks labelled a, b, c, d, e, f, g, h, i and j.

We need to find the number of different routes to travel from station X to station Y, but never using a track twice.  We are allowed to pass through a station multiple times though.

Let's write a route as a sequence of stations and tracks.  E.g. XaPiR means start at station X, go over track a to station P, then over track i to station R.

Possible valid routes from X to Y are:
XaPiRdY or XaPeQgPiRjPbQcRdY

But the route XaPiRjPiRdY is not allowed since we pass over track i twice.

If you try to list the allowed routes by hand, you soon find it is very tedious and long.  Indeed, there are a total of 2501 allowed routes from X to Y!  A surprisingly very large number for such an apparently simple railway system.  To find the answer, we need to write a program.

Preparation

Before starting to write the program, we have to encode the railway system in some way.  I did it in two tables:  one holding for each station the tracks that depart from it (are connected to the station):

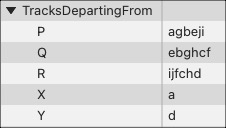
The other table gives for each track the stations at both ends:

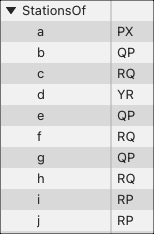
Obviously we can compute one table from the other, either one is sufficient to define the railway system completely.  But it is easier to write the code if we have both available.

Some LiveCode quirks

The code in this page is LiveCode.  LiveCode has very few data types.  Most variables are of type “string of character”.  Thus a lot of the information is encoded in character strings.

There are also associative arrays, numbers, and Booleans (true/false)

Character strings can contain carriage-return characters, noted CR, and their structure can be addressed in many ways, such as:

word 4 of line 3 of S

where S is a character string variable, its lines are separated by returns and words by spaces.  There is also the concept of an “item”, where items are by default separated with commas.  In the code below there is some use of the tab character for separating items.

Recursive solution

We put ourselves at a particular station A and choose one of the tracks t departing from it. The number of routes from that station A is 0 plus the number of routes from the station B at the other end of the chosen track t.  If more than one track departs from A, then we have to examine them one after another (in a loop).

However, before we compute the number of routes from B, we must remove the chosen track t from the still unused tracks, because we may travel a track only once in a route.

The code could be like this:

The function is given two parameters: the station we start from, and the tracks still available (i.e. not yet used) for this route in the network.  In line 3 we consult the table to get the list of tracks departing from the given station.  Then we loop through all of these, and in line 10, for any of them that is still unused, we add the number of routes from its destination station.  Line 5 tests if the track is still usable, line 9 removes it from the usable ones for the duration of the recursive computation in line 10, and puts it back in line 11.

Lines 6 to 8 check if perhaps we have arrived in the end station Y, in which case we found a route and add it to the total number of routes.

There is a small trick here:  the function Destination(Station,Track) looks at the table StationsOf to find the station at other end of a track.  It is of little importance here, but looks like this:

That is because the array StationsOf keeps a string of two letters, and the destination is the letter remaining after removing the letter of the station we started from.

Iterative solution

The iterative solution is perhaps somewhat easier to grasp, but not as easy to code.  A working version is:

To understand this code, let us first look at a much simpler railway system:

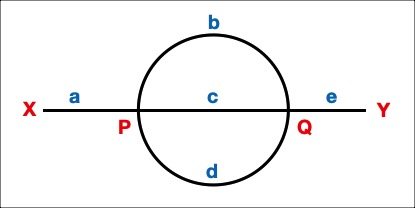
There are stations at the points labelled X, P, Q and Y.  The railroad lines between the stations are labelled a,b,c,d,e.  The system is simple enough that we can draw the complete tree structure representing all routes (remember that the tree for the given system has 2501 routes!).  The nodes of the tree have station names and the branches have track names.  A station name may be used in multiple nodes but a track name may only be used once in a route.  The root of the tree is a node with name X, a route is any path from the root node to a leaf node with name Y.

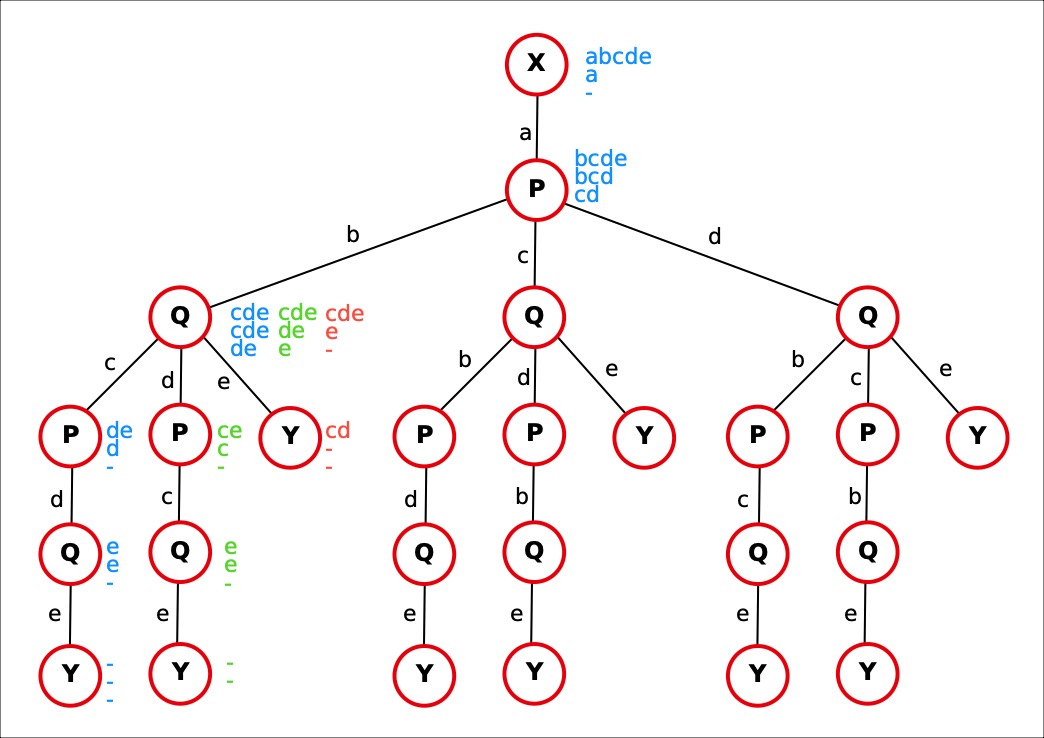
There are “only” nine routes for this simpler railroad system.

We will look at what happens if we take the leftmost route:  from the root X via track a to station P, then left via b to Q, again left via c to P, then Q again, finally Y.  This is the route where the station nodes have blue text alongside them.

The blue texts have three lines:  the list of unused tracks at a given station in a given route, the list of choices at that station, and the choices left after having made a choice.

Starting at the root node X we still have all tracks unused, the first blue line tells us abcde.  But comparing that with the set of tracks leaving X (which, from our table TracksDepartingFrom, is just a), we have only one choice that is common:  track a.  This is the second line of blue text next to station X.  We go down track a, and remove it from the choices, leaving nothing, which is noted in the third line by a hyphen.

We arrive in station P.  Tracks bcde are still unused at this point (first line next to P).  At P we can take one of three different choices:  track b or c or d.  All of them arrive in station Q of course (and note that since we have used track a, it no longer occurs in the set of choices)

Let's go along the first one, track b.  We remove it now from the choices possible in station P, leaving only cd in the third blue line.

We end up in Q, but have used track b, so the remaining unused tracks in Q are now cde.  The tracks departing from Q are bcde, and comparing that with the unused ones we can only choose from cde.

We choose again the first of these, c (and remove it from the choices).  That leads us to P again, but it is a different node in the route.  We now only have de unused but a departing set of abcd.  So we are left with d.  And end up in Q again.  There we can now only use e, ending up in Y and have found a route.

Now comes the tricky bit: when we got to Q the first time, we chose to leave via c, but we still need to explore leaving via d or e.

There could be various ways of remembering that these choices have not yet been explored.  I chose to store them in an array variable, called AvailableChoices in the program code.  To use this, we “backtrack”, i.e. we go back over the route we travelled until we find a node where there are still choices.  This is the reason why we must meticulously remove the used choice at each station.

Backtracking:  we go back from Y to Q, find there are no choices left (hyphen in last line), backtrack again to P, where there are also no choices left, and back to Q again, where there are still de left after having used c.

The thing to do then is to choose d, but remove it from the remaining choices.  That gives the text in green to the right of the blue text:  just e is now left.  Then we arrive at P again where the available tracks are ce (green text), with only c left as choice, so down to Q and finally Y again.  Another route.  And then we have to backtrack again, up to Q where now the only unexplored choice is e, which leads directly to Y, yet another route (red texts).  Having done that, everything at Q was explored and we have to backtrack to P where we can choose c, and so on.

Code

The code should now be readable.  The difficult bit is to realise that going around the loop we must distinguish between choosing+progressing, and backtracking.  Indeed, when just choosing we need to remove the choice taken from the AvailableChoices array, but when we are backtracking we must load the choices from the element of that array.

There is a further check to be made during backtracking:  if we end up back in station X we must stop because we have explored everything.  Actually the test should be about arriving back at X with no choices left.

The array AvailableChoices gets one element added each time we can make a choice.  This array functions much like the recursion stack in the recursive version.

QUESTION: is it possible to have routes ending in a node with a different name than Y?

This is certainly true if we remove track c from the configuration: the path XaPiRjPeQgPbQfRhQ then ends in Q with no tracks leaving Q that have not yet been used.